The Mighty Deuce-Four on "No Gamble No Future"

 

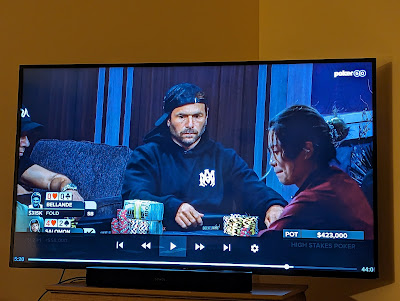
Deuce-Four defeats Jean-Robert Bellande

 In the latest episode of "High Stakes Poker," Rick Salomon raised with deuce-four, Bellande three-bet with pocket queens, and Salomon quickly re-raised all-in. After agonizing a bit, Bellande folded. 

And this is Bellande's face after Salomon showed: 

Now, this doesn't make sense. If Bellande were any good at poker, he would be exhibiting relief. He would know that QQ doesn't stand a chance against 2-4, and that he made the right decision. 

ChatGPT knows nothing about poker

I asked it this: "Is deuce-four a strong starting hand in no-limit hold'em poker?"

It replied: 

The strength of any starting hand in no-limit hold'em poker depends on various factors such as your position at the table, your opponents' tendencies, the stack sizes, and the stage of the tournament or cash game.

That being said, deuce-four is generally considered to be one of the weakest starting hands in no-limit hold'em. It is unlikely to make strong pairs or straights, and it can be easily dominated by higher pairs or stronger hands. In most cases, it is not a hand that you would want to invest a lot of chips in, especially in early or middle positions.

Of course, there may be some situations where deuce-four can be played profitably, such as in late position or against weaker players who are more likely to make mistakes. However, in general, it is not a hand that you would want to rely on to win big pots in no-limit hold'em poker.

A betting paradox that might make your head hurt

 I read about this paradox in a Scientific American article, and could not believe it was true until I had played around with the numbers for a while. It still bothers me, even though I've accepted it. 

Suppose a casino has introduced a new table game they call "17/20." You put a bet down--let's say $100. They flip a fair coin--a genuinely random, 50/50 chance of heads or tails. If it's heads, you win 20% of your bet. If it's tails, you lose 17% of your bet. 

Sounds great, right? It's obviously +EV to play, because you'll either win $20 or lose $17. That's a positive EV of $1.50. 

Now consider what happens if you play twice, and one time it's heads, the other time it's tails. If heads comes first, you now have $120. But then the next toss is tails, so you lose 17% of $120, which is $20.40, leaving you with $99.60--less than you started with. 

If tails comes up first, you lose $17, leaving you with $83. Then it's heads, and you win 20% of that, or $16.60. Now you have $99.60--the same as when it went heads then tails. This shows that it doesn't matter what order the wins and losses come in. 

Even if you win exactly half the time and lose exactly half the time, you still bleed your money away to the house over time. And that is so even though each potential win is greater than each potential loss, before the coin is tossed. 

So this is the paradox: The game is +EV to play once, but -EV to play more than once. The reason is pretty straightforward: 17% of $120 (your loss on the second toss in the head-then-tails scenario) is a larger amount than 20% of $100 (your win on the first toss). And 17% of $100 (your loss on the first toss in the tails-then-heads scenario) is a larger amount than 20% of $83. 

You could fiddle with the percentages and change the long-term outcome. If a win is defined as 20% of your bet, the break-even point will be if a loss is 16.666...% of the bet. Any more than that, and the game is a loser. Below that, it's +EV in the long run. 

Now, I think you could game it so that you're effectively resetting it each time to be like the first toss. That is, if your first toss is a win, you take the $20 profit off the table and bet $100 again. If the first toss is a loss, you add $17 from your pocket and bet $100 again. With a balanced number of heads and tails, and each heads a $20 profit and each tails a $17 loss, you should make money over time. But I think we have to assume that the casino's rules wouldn't allow that, since they're not going to spread any game that's that easy to beat. (Let's not quibble over exactly how the rules would be written or enforced; this is just a hypothetical exercise.) But if you leave the money on the table untouched, and keep playing, it will eventually disappear into the casino's coffers. 

I was hugely surprised by this. I would not have thought it possible to devise a game--especially one so simple--that is +EV to play once, but -EV to play more than once. 

Addendum, May 24, 2021 

You'll need to read the discussion in the comments below for this to make sense. My commenters have caused me to rethink and recalculate. I did so in an attempt to show why they were wrong--but that's not exactly what happened. 

There are a few different pieces to this. 

The two-toss strategy

In the OP, I said that the game would be +EV to play one toss, but -EV for more than one. So suppose you walk into this casino every day and, starting with $100 on the table, play for exactly two coin tosses--no more, no less--then quit for the day. What would be your long-term results? 

As the commenters point out, there are four equally probable outcomes: HH, HT, TH, and TT. Over the long run, those should happen equally often. The net profits/losses are, respectively, +44, -0.40, -0.40, and -31.11. The sum of those is +12.09, an average of $3.02 per day profit, or $1.51 per coin toss. 

Interestingly, that's a hair more than the $1.50 profit per toss that we would calculate to be the EV of playing one toss and quitting. Which suggests that playing the two-toss strategy is more profitable. 

The three-toss strategy

So I went to the obvious next step: Suppose I always play three tosses per session. Now there are 8 equally probable outcomes. One outcome is HHH, which yields +72.80. One is TTT, which yields -42.82. There are three combinations with two heads and one tails, each of which is +19.52. there are three combinations with one heads and two tails, -17.33. Add all those up, and it's +36.55, for an average profit of $4.57 per day, or $1.52 per toss. 

So now it appears that the 3-toss strategy is more profitable--both per day and per toss--than the 2-toss strategy, which in turn is more profitable than the 1-toss strategy. 

This is not what I expected. 

Asymmetry 

As the commenters point out, the difference lies in the outcomes when you don't have an exactly 50/50 split in heads and tails. It's clearly, demonstrably true that any session you play in which the heads and tails are exactly evenly divided results in a net loss. E.g., playing 8 tosses, with 4H and 4T (in any order) yields a net loss of $1.59 on the initial $100 bet (again, with all the money left on the table until the end). 

But the interesting part happens in the asymmetrical outcomes. On the rare occasion that you play an 8-toss strategy and get all 8 tails, you're left with $22.52 on the table at the end, for a loss of $77.48. But you will equally often get a run of all 8 heads, at the end of which you will have $429.98 on the table, for a profit of $329.98. The probabilities are symmetrical, but the outcomes are decidedly asymmetrical. The same sort of thing is true for each balanced pair of possible outcomes, e.g., 7H1T/7T1H, or 5H3T/3H5T. 

In fact, if you extend the idea to, say, a 1000-toss strategy, you'll quickly realize that many days you'll lose the entire starting $100 (assuming that the casino doesn't deal in bets of a fraction of a penny) long before the thousandth toss. Your losses are capped at $100, but your wins are potentially unlimited. 

This is, I now think, the key consideration. I was previously assuming that an exactly 50/50 split was the most likely, and since the probabilities of uneven heads/tails splits were symmetrical, those could just be disregarded. 

Long sessions

With that in mind, I set up an Excel spreadsheet to simulate a 10,000-toss strategy, and ran it 20 times. I kind of suspect that Excel's random-number generator is a little wonky, because I got 15 outcomes with more than 5000 heads, and only 5 with less. But that doesn't matter for present purposes. 

In 13 trials, I had a fraction of a cent left--call it zero. In five trials, I had less than $1 left. These included, e.g., 5038 heads leaving me with $0.24, and 5041 heads leaving me with $0.73. (Remember that because an exactly even 50/50 distribution is always a loss, you have to be well above the average number of heads to ever leave with a profit.) 

But in two trials, I had hugely positive results. In one that had 5086 heads (and, of course, 4914 tails), the final amount on the table was $11,629,561! And in one extremely improbable trial, the spreadsheet somehow came up with 5125 heads, yielding--you'd better be sitting down for this--$20 trillion! 

Now, that's another outcome that makes me suspect Excel's RNG, because getting 5125 heads out of 10,000 tosses has a probability of only about 0.0064. (I used this online binomial calculator to get that number.) But the point is that in long sessions in which luck favors you with substantially more heads than tails, you can win huge amounts, while in the equally probable sessions with substantially more tails than heads, you still lose only $100 each time. 

Conclusion 

I think I was wrong about how to calculate the EV of the game beyond a single toss--as was the author of the Scientific American article. And I appreciate the two commenters for pressing me to look deeper. 

Addendum, May 24, 2021 

Not all Scientific American articles are available online, but the one that started this for me happens to be. "Is Inequality Inevitable?" by Bruce M. Boghosian: https://www.scientificamerican.com/article/is-inequality-inevitable/

Here's the relevant section: 

In 1986 social scientist John Angle first described the movement and distribution of wealth as arising from pairwise transactions among a collection of “economic agents,” which could be individuals, households, companies, funds or other entities. By the turn of the century physicists Slava Ispolatov, Pavel L. Krapivsky and Sidney Redner, then all working together at Boston University, as well as Adrian Drgulescu, now at Constellation Energy Group, and Victor Yakovenko of the University of Maryland, had demonstrated that these agent-based models could be analyzed with the tools of statistical physics, leading to rapid advances in our understanding of their behavior. As it turns out, many such models find wealth moving inexorably from one agent to another—even if they are based on fair exchanges between equal actors. In 2002 Anirban Chakraborti, then at the Saha Institute of Nuclear Physics in Kolkata, India, introduced what came to be known as the yard sale model, called thus because it has certain features of real one-on-one economic transactions. He also used numerical simulations to demonstrate that it inexorably concentrated wealth, resulting in oligarchy.

To understand how this happens, suppose you are in a casino and are invited to play a game. You must place some ante—say, $100—on a table, and a fair coin will be flipped. If the coin comes up heads, the house will pay you 20 percent of what you have on the table, resulting in $120 on the table. If the coin comes up tails, the house will take 17 percent of what you have on the table, resulting in $83 left on the table. You can keep your money on the table for as many flips of the coin as you would like (without ever adding to or subtracting from it). Each time you play, you will win 20 percent of what is on the table if the coin comes up heads, and you will lose 17 percent of it if the coin comes up tails. Should you agree to play this game?

You might construct two arguments, both rather persuasive, to help you decide what to do. You may think, “I have a probability of ½ of gaining $20 and a probability of ½ of losing $17. My expected gain is therefore:

½ x ($20) + ½ x (-$17) = $1.50

which is positive. In other words, my odds of winning and losing are even, but my gain if I win will be greater than my loss if I lose.” From this perspective it seems advantageous to play this game.

Or, like a chess player, you might think further: “What if I stay for 10 flips of the coin? A likely outcome is that five of them will come up heads and that the other five will come up tails. Each time heads comes up, my ante is multiplied by 1.2. Each time tails comes up, my ante is multiplied by 0.83. After five wins and five losses in any order, the amount of money remaining on the table will be:

1.2 x 1.2 x 1.2 x 1.2 x 1.2 x 0.83 x 0.83 x 0.83 x 0.83 x 0.83 x $100 = $98.02

so I will have lost about $2 of my original $100 ante.” With a bit more work you can confirm that it would take about 93 wins to compensate for 91 losses. From this perspective it seems disadvantageous to play this game.

Addendum, June 10, 2021 

I emailed the author of the article about my concerns. He responded, saying that many people had raised similar questions, so when the article was reprinted in a book, he took the opportunity to revise the section in question for greater clarity. 

 Here's the relevant portion of the revised version of the article he sent me: 

(The revision is posted here with Mr. Boghosian's kind permission. Source: B.M. Boghosian, “The Inescapable Casino”, reprinted in “The Best Writing on Mathematics 2020”, M. Pitici ed., Princeton University Press (2020).)

This revision sounds correct to me: the EV is positive, but you'll lose more often than you'll win. I still quibble with the last sentence, that "it seems decidedly disadvantageous to play this game." I mean, there's a sense in which that's true, but only if you're tallying wins and losses, while taking no account of their magnitudes--which seems like not the best method of accounting. It was this sentence that made me think that Mr. Bohosian was saying that the game's EV was negative when played more than one toss. I see now that that wasn't actually what he was trying to say. 

Of course, you have to be able to tolerate the losses without going broke. In his email to me, Mr. Boghosian mentioned the Kelly criteria for determining what fraction of one's bankroll can be risked. I think Kelly's formula is pretty well known among serious poker players. Phil Laak is particularly vocal about it--e.g, this 2009 Bluff magazine column. For an introduction, see here or here. 

 

What are the odds?

 Yesterday Poker News published this article about a remarkable hand at the final table of an event in the Lone Star Poker Series. It was all-in pre-flop, Troy Clogston's JsJh against short-stacked Don Iyengar's AdJc. Nothing remarkable about that, or about the way the board fell. What was remarkable was Clogston calling every card of the board before seeing it. Read the article and watch the embedded video there for the details of how it played out. 

Last night I was telling Nina about this. She asked what the probability was. Offhand, I guessed one in a million. This was an actual quick estimate on my part, not just thoughtlessly spouting the cliched "one in a million." Nina thought that was low by an order of magnitude--more like one in ten million. 

So I decided to do the math and see. As I write these words, I still haven't done the calculation, so I don't know the answer. By the time I finish this post, I will. 

We start with the flop. Clogston called for 8-9-10 rainbow. (I don't actually hear "rainbow" in the video, because the announcer talks over it, but I'm assuming it's there, as the text of the article says.) The flop not only comes 8s9h10c, but in that exact order. Now, I don't think the order matters, because surely everybody would give him credit for the call even if the order had been different. So let's ignore the left-to-right order. With 48 unknown cards, and none of the known cards being of the three ranks in question, what is the probability of this guess? 

There are 17,296 different ways of drawing three cards from a deck of 48. (You can find a combination/permutation calculator here.) There are 24 different ways of assembling 8-9-10 rainbow. (Each of four 8s can be matched with each of three 9s and each of two 10s, and 4 x 3 x 2 = 24.) So 24 of the possible 17,296 combinations would fulfill the first guess. Probability: 24/17,296 = 0.001388. This equals about 1 in 720. 

Now we're to the turn. We have 45 unseen cards remaining. So guessing one is the straightforward probability of 1/45, or 0.02222. 

On the river, it's 1/44, or 0.02273. 

For Clogston to get all three components of his guess correctly, we have to multiply those three probabilities: 0.001388 x 0.02222 x 0.02273 = 0.0000007010. This equals 1 in 1,426,000. 

So under the conditions as specified here, my guess was the closer one--and not too far off, for taking only a few seconds to think about it. 

However, perhaps you disagree with my decision about the order of the flop. If you want to make the challenge harder by saying that you would only accept Clogston's guess as correct if he got the order of the 8, 9, and 10 correct, it adds extra difficulty. 

Out of 48 cards, the first card must be an 8; probability 4/48, or 0.08333. The second card must be one of three nines that doesn't match the suit of the 8; probability 3/47, or 0.06383. The third card must be one of the two tens that doesn't match either of the previous suits; probability 2/46, or 0.04348. All three of those must be true simultaneously, so again we have to multiply the independent probabilities together. 0.08333 x 0.06383 x 0.04348 = 0.0002313. This equals about 1 in 4324. (A faster way to get the same result is to realize that you have the same 24 winning ways to make 8-9-10 rainbow, but now we're talking about permutations instead of combination, and a permutation calculator says that there are 103,776 unique orders of three cards that can be drawn from a deck of 48 cards. 24/103,776 works out to 1/4324 exactly.) 

If you now multiply that by the turn and river probabilities calculated previously (they are unchanged for this), you get 0.0000001168, or about 1 in 8,560,000. That is much closer to Nina's guess than to mine. 

So who won our little guessing game? As the classic poker answer goes, "It depends."